Analiza determinantów przepływów handlowych na świecie w latach 2000–2020 z wykorzystaniem modeli grawitacyjnych
Streszczenie: Niniejsza praca ma na celu sprawdzenie czynników wpływających na wielkość przepływów handlowych pomiędzy dwoma państwami. Wykorzystano do tego rozszerzony model grawitacyjny oraz następujące narzędzia ekonometryczne: modele Fixed Effects (FE), Correlated Random Effects (CRE) oraz Poisson Fixed Effects (PFE), szacowany metodą Poisson Pseudo Maximum Likelihood (PPML). Każdy model uzasadniono teoretycznie oraz dołączono do pracy replikowalne kody w R do sprawdzenia poprawności obliczeń. Zweryfikowano następujące hipotezy: 1) tradycyjne zmienne (PKB eksportera i importera oraz odległość między państwami) są istotnymi predykatorami poziomu handlu; 2) zamożność społeczeństwa mierzona PKB per capita pozytywnie wpływa na wymianę handlową; 3) wspólna granica zwiększa handel; 4) należenie państwa do Unii Europejskiej pozytywnie wpływa na jego eksport; 5) wspólny język i historia (przeszłość kolonialna) pozytywnie wpływają na wzajemny handel; oraz 6) podobieństwo systemów prawnych zwiększa wymianę handlową. Wykazano, że nie ma podstaw do odrzucenia hipotez 2), 3), 5) i 6). Analiza wpływu odległości na handel oraz członkostwa importera w UE jest bardziej zniuansowana.
Słowa kluczowe: handel międzynarodowy, dane panelowe, model grawitacyjny handlu, model Poisson Fixed Effects, model CRE, model efektów stałych.
JEL: F14, C33, C51
Analysis of Trade Flows’ Determinants from 2000 to 2020 Using Gravity Models
Summary: This study aims to examine the factors influencing the volume of trade flows between two countries. An extended gravity model was utilized along with the following econometric tools: Fixed Effects (FE), Correlated Random Effects (CRE), and Poisson Fixed Effects (PFE) estimated with Poisson Pseudo Maximum Likelihood (PPML). Each model was theoretically justified, and replicable R codes were included to enable the correctness of the calculations to be checked. The study tested the following hypotheses: 1) traditional variables (GDP of the exporter and importer, as well as the distance between countries) are significant predictors of trade levels; 2) societal wealth, measured by GDP per capita, positively influences trade; 3) a shared border increases trade; 4) membership in the European Union positively impacts a country’s exports; 5) a common language and shared history (colonial ties) positively influence bilateral trade; and 6) similarity in legal systems increases trade exchange. The analysis confirmed that there is no basis for rejecting hypotheses 2), 3), 5), and 6). The impact of distance on trade and the importerʼs EU membership proved to be more nuanced.
Keywords: international trade, panel data, gravity model of trade, Poisson Fixed Effects model, Correlated Random Effects, Fixed Effects.
Wstęp
Modele grawitacyjne to niezwykle użyteczne narzędzie do analizowania determinantów handlu. W literaturze spotyka się artykuły wykorzystujące ten model w odniesieniu do jednego państwa (Cieślik 2018; Ambroziak 2018), członków organizacji międzynarodowej (Drzewoszewska i in. 2013; Maciejewski 2017; Pietrzak i Łapińska 2014), państw z określonego regionu świata (Golovko, Sahin 2021; Klimczak 2015), a nawet do jednostek administracyjnych w ramach jednego państwa (Mroczek i in. 2014). Tematycznie model grawitacyjny handlu wykorzystywany jest zazwyczaj do analizowania ogółu przepływów handlowych między państwami, aczkolwiek coraz częściej badacze skupiają się na jednym sektorze dóbr, np. rolniczych (Sapa, Droždz 2019) lub żywieniowych (Sapa, Kryszak 2021), albo nawet na pojedynczym dobrze, np. zbożu (Kułyk, Augustowski 2018) czy miodzie pszczelim (Popovych 2018).
Od strony praktycznej przeprowadzenie poprawnie metodologicznego badania ekonometrycznego z zastosowaniem powyższego modelu nie jest oczywiste. Najpopularniejsza analiza, która brałaby pod uwagę zarówno przekrojowy, jak i czasowy aspekt analizowanych danych, wymagałaby oszacowania modelu panelowego. Jako że analizie poddaje się całą populację (wszystkie województwa Polski, wszystkich członków Unii Europejskiej itp.), a nie losowo wybraną próbkę, to wskazane byłoby skorzystanie z modelu efektów stałych – ang. Fixed Effects – FE (Baltagi 2021, s. 12). Podejście to obarczone jest jednak pewnymi problemami. Po pierwsze, modelem FE nie można szacować wpływu czynników stałych w czasie na zmienną objaśnianą. Po drugie, przy stosowaniu logarytmów zmiennych wskazane jest wykluczenie obserwacji zawierających zerowe wartości (brak handlu pomiędzy dwoma państwami), co jednak wiąże się z arbitralnym założeniem, że zerowe obserwacje nie niosą żadnej istotnej wiadomości do modelu.
W pracy zaprezentowano dwa sposoby na rozwiązanie powyższych problemów. Poza modelem Fixed Effects (FE) zastosowano Correlated Random Effects (CRE) i Poisson Fixed Effects (PFE) będący szacowaniem modelu FE metodą Poisson Pseudo Maximum Likelihood (PPML). Modele oszacowano w programie R, a wszystkie zawarte w artykule obliczenia są w pełni replikowalne. Kody i dane udostępnione są w otwartym repozytorium: https://github.com/tymoteuszmetrak/gravity_article.
Poza problemami natury ekonometrycznej zajęto się weryfikacją kilku hipotez badawczych dotyczących determinantów handlu międzynarodowego. Sformułowano je na podstawie dotychczasowej literatury, biorąc pod uwagę zwłaszcza zmienne „typowego modelu grawitacyjnego” zaproponowane przez Heada i Mayera (2014) oraz główne przeszkody handlowe zebrane przez Bergstranda i Eggera (2013). W dalszej części artykułu znajduje się szersze omówienie badań będących podstawą stawianych hipotez. Weryfikacja niektórych z nich nie byłaby możliwa bez zastosowania modeli CRE i PFE. Badane hipotezy to:
- H1: tradycyjne zmienne (PKB eksportera, importera i odległość między państwami) są istotnymi predykatorami poziomu handlu;
- H2: zamożność społeczeństwa mierzona PKB per capita pozytywnie wpływa na wymianę handlową;
- H3: wspólna granica zwiększa handel;
- H4: należenie państwa do Unii Europejskiej pozytywnie wpływa na jego eksport;
- H5: wspólny język i historia (przeszłość kolonialna) pozytywnie wpływają na wzajemny handel;
- H6: podobieństwo systemów prawnych zwiększa wymianę handlową.
1. Model grawitacyjny – teoria
Socjolodzy i ekonomiści od co najmniej XIX w. zaczęli aplikować prawo powszechnego ciążenia Newtona do modelowania zjawisk społecznych. Jak podaje Chojnicki (1966), analizowano w ten sposób zwłaszcza migracje, popyt i podaż na produkty pomiędzy ośrodkami miejskimi oraz „siłę przyciągania” konsumentów do miast. Jednak to przede wszystkim wykorzystanie modelu grawitacyjnego do analizy handlu światowego trwale wpisało się do kanonu badań ekonomicznych.
Model grawitacyjny handlu w podstawowej formie cechuje się dużą prostotą oraz intuicyjnością. Zakłada on, że wielkość wymiany handlowej między państwami jest wprost proporcjonalna do wielkości ich gospodarek (wyrażonych zwykle jako PKB) i odwrotnie proporcjonalna do odległości (Tinbergen 1962). Można go przedstawić jako:
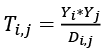
gdzie:
Ti,j – wielkość wymiany handlowej między państwem i oraz j,
Yi – PKB państwa i,
Yj – PKB państwa j,
Di,j – dystans pomiędzy państwami i oraz j.
Model taki nie pozwala jednak na analizę wpływu innych czynników na wielkość wymiany handlowej, a także czyni kilka założeń, m.in., że koszty handlowe zależą wyłącznie od odległości dwóch państw, a podaż i popyt na dobra są zależne wyłącznie od wielkości gospodarek. Po uchyleniu tych założeń można szacować model postaci:
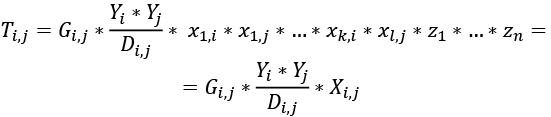
gdzie:
Gi,j – to tzw. stała grawitacyjna – stała dla danego połączenia handlowego,
xk,i – k-ta zmienna wpływająca na handel i,
xl,j – l-ta zmienna wpływająca na handel j,
zn – n-ta zmienna wpływająca na wzajemny handel między i oraz j,
Xi,j – wektor zmiennych wpływających na handel i, lub handel j, lub handel między i oraz j.
Istnieją jeszcze bardziej zaawansowane modele: strukturalny model grawitacyjny, modele z CES funkcją popytu itp. Istotny przegląd literatury w tym temacie przeprowadził Anderson (2011). Jednakże już dzięki powyższej modyfikacji tradycyjnego modelu grawitacyjnego handlu można szacować wpływ na handel takich zmiennych, jak wspólna granica, należenie do Unii Europejskiej, poziom PKB per capita i inne.
2. Przegląd literatury
Modele grawitacyjne handlu są jednymi z kilku popularnych modeli ekonometrycznych, służących do analizy handlu międzynarodowego. Warto wspomnieć chociażby o modelach Ricardo, Heckschera-Ohlina, Krugmana czy Dixita-Stiglitza. Pomimo takiej różnorodności dostępnych narzędzi model grawitacyjny pozostaje użyteczny; do takich wniosków doszedł ostatnio m.in. Klimczak (2015). Ogromnymi zaletami tego modelu są prostota i możliwość elastycznego kształtowania założeń co do funkcji konsumpcji.
Głównym zagadnieniem w odniesieniu do badanych modeli grawitacyjnych są determinanty przepływów handlowych. Przykładowo, Maciejewski i Wach (2019) dla państw Unii Europejskiej wykazali, że pozytywnie na handel wpływają PKB eksportera i importera, wspólna granica oraz członkostwo pary krajów w UE. Posiadanie wspólnej waluty euro na handel oraz PKB per capita eksportera miało nieoczywisty wpływ na handel. W ich badaniu odległość oddziaływała na handel negatywnie w sposób istotny statystycznie. Golovko i Sahin (2021) oszacowali modele PFE dla 86 państw Euroazji. Wykazali, że posiadanie wspólnej granicy i posługiwanie się tym samym językiem istotnie statystycznie zwiększa wzajemny handel między państwami. W ich modelach oszacowania przy logarytmie PKB per capita eksportera i importera były pozytywne i istotne statystycznie, tak samo jak należenie do Światowej Organizacji Handlu i regionalnych porozumień handlowych.
Liczba artykułów w analizowanym temacie w literaturze anglojęzycznej jest tak duża, że warto odwołać się do opracowań zbiorczych. W swoim artykule przeglądowym Kepaptsoglou i in. (2010) zwrócili uwagę, że w pierwszej dekadzie XXI w. jednym z najczęściej analizowanych tematów za pomocą modeli grawitacyjnych były efekty porozumień o wolnym handlu. Wyniki badań nie były zgodne, aczkolwiek pewna ich część zidentyfikowała pozytywny wpływ porozumień o wolnym handlu (np. NAFTA, UE, ASEAN) na wymianę handlową wewnątrz porozumienia i relatywny jej spadek z partnerami zewnętrznymi. Bergstrand i Egger (2013) skupili się wprost na przeszkodach w handlu badanych modelami grawitacyjnymi. „Naturalne” przeszkody, które bezpośrednio wpływają na koszty transportu dóbr to, zdaniem autorów, m.in.: odległość, średni czas wymagany do transportu dóbr drogą morską, brak wspólnej granicy i brak dostępu do oceanu światowego. Przeszkody „sztuczne” to przede wszystkim cła i brak członkostwa w porozumieniach o wolnym handlu, ale też nadmierne wymogi regulacyjne. Obecność tych przeszkód lub ich intensywność (np. większa odległość, wyższe cała) negatywnie wpływa na handel wzajemny między państwami.
Prawdopodobnie największą metaanalizę dotyczącą modeli grawitacyjnych handlu przeprowadzili Head i Mayer (2014). Po przeanalizowaniu 159 artykułów zidentyfikowali tzw. „typowy model grawitacyjny”. Z ich badań wynika, że zmienne, które najczęściej pozytywnie wpływały na wielkość wzajemnej wymiany handlowej, to PKB importera i eksportera, wspólna granica, posługiwanie się tym samym językiem, powiązania kolonialne, istnienie porozumienia o wolnym handlu, członkostwo w UE, członkostwo w NAFTA oraz posługiwanie się tą samą walutą. Negatywnie na handel oddziaływała odległość między państwami.
Podobne wnioski płyną z literatury polskojęzycznej. Warto przytoczyć jednak kilka badań. Drzewoszewska i in. (2013) przeanalizowali wymianę handlową między państwami Unii Europejskiej w latach 1999–2010. W ich modelu PKB eksportera i importera pozytywnie wpływały na handel, a odległość negatywnie. Klimczak (2015) w analizie państw Bałkanów Zachodnich pokazał pozytywny wpływ PKB eksportera oraz jego populacji na handel. Co ciekawe, w jego badaniu PKB importera miało negatywny wpływ na handel, podobnie jak jego populacja i odległość fizyczna między państwami. Współczynnik przy odległości zmieniał jednak znak po dodaniu do modelu innych zmiennych, oddających bliskość językową, religijną, występowanie wspólnej granicy i stan wojny między krajami. Wojna wpływała negatywnie na wymianę handlową w danym roku oraz rok po zakończeniu, a pozostałe wymienione zmienne oddziaływały w sposób pozytywny. Cieślik (2007) zbadał wymianę handlową Polski z partnerami i wykazał pozytywny wpływ porozumień o wolnym handlu zarówno wielostronnych (Układ Europejski, EFTA i CEFTA), jak i bilateralnych (z Chorwacją, Estonią, Izraelem, Litwą, Łotwą, Estonią i Turcją) na wielkość wzajemnych obrotów handlowych. Co ciekawe, pozytywnie na wymianę wpływała też bliskość językowa (grupa języków słowiańskich). W badaniu powtórzonym dekadę później Cieślik (2018) oszacował pozytywny skutek dołączenia Polski do Unii Europejskiej na wielkość bilateralnych obrotów handlowych.
3. Dane
Do niniejszego badania wykorzystano powszechnie używaną bazę „CEPII – Gravity” (Conte, Cotterlaz, Mayer 2022). Zawiera ona dane dla 252 państw i terytoriów, które istniały na przestrzeni lat 1948–2021. Każdy wiersz w bazie oznacza przepływ handlowy pomiędzy państwem eksportera (origin) a importera (destination) w danym roku. Poza danymi odnośnie do handlu w bazie zebrano dane dotyczące odległości pomiędzy państwami (w tym odległościami ważonymi populacją), PKB, PKB per capita, populacji, posiadania wspólnej granicy, przeszłości kolonialnej, porozumień handlowych, uczestnictwa w Światowej Organizacji Handlu, posługiwania się tym samym językiem, posiadania wspólnie jednego państwa-przodka itd. Łącznie w bazie zebrano ponad 100 zmiennych, a liczba obserwacji przekracza 4 miliony.
W artykule ograniczono zakres czasowy do lat 2000–2020. Dla roku 2021 (najnowszego w bazie) obserwacje są niepełne i zawierają bardzo wiele brakujących wartości NA, dlatego zdecydowano się na ich usunięcie. Nie wzięto pod uwagę wartości sprzed roku 2000 z dwóch powodów. Po pierwsze, tam również znajdowało się wiele braków danych, co utrudniłoby analizę. Po drugie, to w czasach najnowszych popularna jest idea, że „odległość nie ma znaczenia” z powodu rozwoju technologii komunikacyjnych i informacyjnych. Zgodnie z hipotezą H1 dystans nadal powinien mieć znaczenie, a do jej weryfikacji potrzeba stosunkowo współczesnych danych. Odległość brana pod uwagę w niniejszym badaniu to tzw. dystans ważony populacją. Jest to wskaźnik odległości wyrażony w kilometrach, który bierze pod uwagę rozproszenie populacji w obu krajach i jest bardziej wiarygodny od indeksów, które mierzą odległość jedynie między stolicami lub między dwoma największymi miastami państw. Dystans ważony populacją bierze pod uwagę wszystkie miasta w danym kraju o populacji większej niż 300 000 osób[1] (Conte i in. 2022). Wyliczany jest według wzoru:
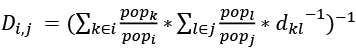
gdzie:
Di,j – dystans między państwami ważony populacją,
popk – populacja k-tego miasta w kraju i,
popl – populacja l-tego miasta w kraju j,
popi – suma populacji wszystkich dużych miast w państwie i,
popj – suma populacji wszystkich dużych miast w państwie j,
dkl – odległość między miastem k oraz l.
Dzięki takim przekształceniom zmienna odpowiadająca za odległość bierze pod uwagę rozproszenie populacji i jej strukturę geograficzną. Przykładowo, odległość między największymi miastami Polski i Niemiec (Berlin i Warszawa) wynosi 518 km, a dystans ważony populacją między oboma państwami w 2020 r. wyniósł 575 km.
W ramach dalszych przekształceń z otrzymanej bazy usunięto obserwacje, w których odzwierciedlony był handel państwa samego ze sobą (np. metropolii z własnym terytorium zamorskim). Usunięto też obserwacje, dla których brakowało danych co do PKB, odległości, danych o wspólnej granicy, języku i należenia do UE. Następnie podzielono bazę na dwie tabele – jedną, z której usunięto połączenia handlowe, dla których handel wynosił zero i jedną, w której takie wartości zostały zachowane. Potem zostawiono w obu bazach tylko te połączenia handlowe, dla których dostępne są pełne dane za lata 2000–2020, aby otrzymać zbilansowany panel. Na sam koniec wyliczono logarytmy wybranych zmiennych – PKB, PKB per capita i odległości ważonej populacją.
4. Wykorzystane modele
Łącznie oszacowano pięć modeli opisanych poniżej. Pierwsze dwa są modelami bazowymi, które napotykają na dwie podstawowe trudności – niemożliwość szacowania wpływu regresorów stałych w czasie oraz konieczność pominięcia w modelowaniu obserwacji, dla których wielkość wymiany handlowej wynosi 0. Kolejne modele odpowiadają na te trudności i rozwiązują je.
Model 1
Podstawowy model, którego użyto, to model efektów stałych dla każdego połączenia handlowego – model FE. Model taki wymaga addytywnej formy, dlatego konieczne było przekształcenie powyżej omówionego równania poprzez obustronne zlogarytmowanie. Oszacowano zatem model podstawowy postaci:
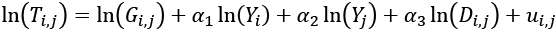
gdzie ui,j to egzogeniczny składnik losowy (który może być skorelowany z jakimkolwiek regresorem).
Zgodnie z hipotezami oczekuje się, że współczynniki α1 i α2 będą dodatnie na poziomie istotności 5%, a α3 przyjmie wartość istotnie ujemną.
Model 2
Aby przetestować pozostałe hipotezy, konieczne było rozszerzenie modelu o dodatkowe zmienne zależne. Oszacowano model postaci:
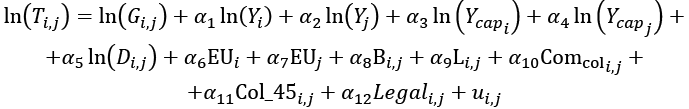
gdzie:
ln(Y_capi) – logarytm PKB per capita w państwie eksportera,
ln(Y_capj) – logarytm PKB per capita w państwie importera,
EUi – zmienna binarna, czy państwo eksportera należało w danym roku do UE,
EUj – zmienna binarna, czy państwo importera należało w danym roku do UE,
Bi,j – zmienna binarna, czy państwa posiadają wspólna granicę,
Li,j – zmienna binarna, czy przynajmniej część populacji obu państw mówi tym samym językiem,
Com_coli,j – zmienna binarna, czy oba państwa miały wspólnego kolonizatora po 1945 r.,
Col_45i,j – zmienna binarna, czy oba państwa znajdowały się w relacji kolonialnej po 1945 r.,
Legali,j – zmienna binarna, czy państwa mają wspólne źródła systemu prawnego.
Powyższy model zawiera jednak dwa problemy. Po pierwsze, niemożliwe jest oszacowanie wpływu zmiennych stałych na zmienną objaśniająca z powodu procedury „uśredniania”. Przykładowo, dla Modelu 1 proces szacowania będzie przebiegał następująco. Najpierw należy obliczyć średnie (po czasie) wszystkich zmiennych po obu stronach równania:
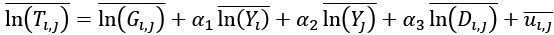
Odejmując teraz to równanie od pierwotnego:
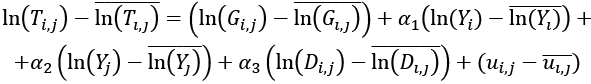
gdzie 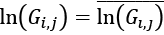 , bo stała jest ze swojej natury stała w czasie. Ich różnica wyniesie zatem zero. Tak samo w procesie uśredniania stanie się z innymi zmiennymi stałymi w czasie. Finalny model, szacowany w modelu efektów stałych (stosując notację, że
, bo stała jest ze swojej natury stała w czasie. Ich różnica wyniesie zatem zero. Tak samo w procesie uśredniania stanie się z innymi zmiennymi stałymi w czasie. Finalny model, szacowany w modelu efektów stałych (stosując notację, że 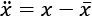 ), będzie miał postać:
), będzie miał postać:
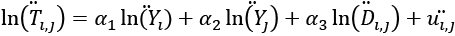
Drugi problem dotyczy logarytmowania zmiennej niezależnej. Poprzez zlogarytmowanie zmiennej „handel” zmuszeni jesteśmy bowiem wyłączyć z naszej próby wszystkie połączenia handlowe, dla których handel był zerowy. Może mieć to wpływ na oszacowania, gdyż stosując takie modele zakłada się a priori, że zerowy eksport jednego państwa do drugiego nie niesie ze sobą żadnych informacji.
Model 3
Rozwiązaniem problemu nr 1, czyli szacowania wpływu zmiennych stałych w czasie, może być model CRE – Correlated Random Effects. Dopuszcza on korelację błędu ze zmiennymi objaśniającymi, a jednocześnie pozwala na otrzymanie oszacowań dla zmiennych stałych w czasie. Oszacowania dla pozostałych zmiennych są identyczne jak w modelu FE (Wooldridge 2021). W praktyce takie estymacje otrzymuje się dzięki dodaniu średnich zmiennych w czasie do modelu i późniejsze szacowanie modelu RE. To pozornie proste przekształcenie zostało zaproponowane niezależnie od siebie przez Mundlaka (1978) i Chamberlaina (1984), ale dopiero od niedawna zyskuje na popularności. Szacowany model będzie miał postać:
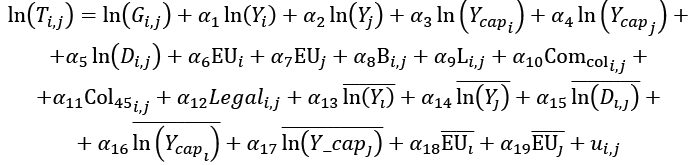
Dotychczas w literaturze polskojęzycznej jako rozwiązanie powyższego problemu wskazywano oszacowanie modelu Hausmana-Taylora (por. Bułkowska 2018, s. 44). Wykorzystali go m.in. Cieślik i Hagemejer (2011), zajmując się kwestią liberalizacji handlu w Europie Środkowej i Wschodniej, oraz Cieślik i in. (2009), badając potencjalne skutki przystąpienia Polski do strefy euro. Model Hausmana-Taylora (1981) zakłada podział zmiennych objaśniających na dwie kategorie: 1) te, które mogą być skorelowane z efektem indywidualnym, oraz 2) te, które na pewno są z nim nieskorelowane. W obu tych grupach mogą pojawić się zmienne stałe w czasie. W celu estymacji współczynników model stosuje najpierw model efektów stałych (FE), aby oszacować część parametrów i uzyskać reszty. Następnie używana jest metoda zmiennych instrumentalnych do estymacji pozostałych parametrów. Dotychczasowe oszacowania parametrów umożliwiają obliczenie reszt, które są z kolei wykorzystywane do wyznaczenia wariancji błędu losowego oraz efektu indywidualnego. Dzięki temu możliwe jest zastosowanie metody najmniejszych kwadratów z korektą (UMNK) w celu uzyskania końcowych estymacji (StataCorp 2023). Poprawne wykorzystanie tego modelu wymaga dużej wiedzy eksperckiej i starannego dopasowania zmiennych do ww. grup. Model CRE nie posiada tych ograniczeń, a ponadto jego oszacowania są łatwo porównywalne z modelem FE.
Modele 4 i 5
Rozwiązaniem problemu nr 2, czyli ograniczenia się do dodatnich wartości handlu, może być model efektów stałych szacowany z rozkładem Poissona – Poisson Fixed Effects (PFE). W literaturze taki sposób estymacji nazywa się Poisson Pseudo-Maximum Likelihood (PPML). Jest to rozszerzenie zwykłego modelu Poissona na dane panelowe. Zmienną objaśnianą jest poziom handlu bez logarytmowania, przez co można wykorzystać zdecydowanie więcej obserwacji. Otrzymane oszacowania są zgodne, a interpretacja oszacowań taka jak w modelach szacowanych MNK – dla zmiennych objaśnianych w logarytmie współczynnik jest elastycznością, a dla zmiennych binarnych jest semielastycznością (Shepherd i in. 2019). Przedstawiając skrótowo, model przyjmuje postać:
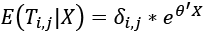
gdzie δi,j to efekt stały (por. stałą grawitacyjną dla połączenia handlowego), θ to wektor współczynników, a X to wektor niestałych w czasie zmiennych objaśniających.
Analogicznie do modelu FE modele PFE też oszacowano w wersji podstawowej (Model 4 tylko z 3 regresorami – logarytmy PKB i odległości) i rozszerzonej (Model 5).
5. Badanie empiryczne
Wyniki oszacowań modelu podstawowego Fixed Effects i Poisson Fixed Effects (Modele 1 i 4) zawiera tabela 1. W obu modelach PKB eksportera i importera pozytywnie wpływają na handel pomiędzy państwem eksportera a importera.
| no data | FE (1) | PFE (4) |
|---|---|---|
| Log. PKB eksportera | 0,53*** (0,01) |
0,50*** (0,00) |
| Log. PKB importera | 0,77*** (0,01) |
0,54*** (0,00) |
| Log. odległości | –0,22 (0,17) |
–0,53*** (0,00) |
| Liczba obserwacji | 291543 | 589176 |
| R2 | 0,25 | brak danych |
| Adj. R2 | 0,21 | brak danych |
| Log Likelihood | brak danych | –9050369788,35 |
| AIC | brak danych | 18100739582,70 |
Objaśnienia: ***p < 0,001; **p < 0,01; *p < 0,05.
Źródło: opracowanie własne.
Jak widać, w modelu efektów stałych co prawda współczynnik przy odległości ma oczekiwany znak, jednakże nie jest on istotny statystycznie. W modelu PFE odległość ma wpływ ujemny i istotny statystycznie na poziomie 0,1%. Różnica we wpływie odległości może wynikać z dwóch powodów. Po pierwsze, model PFE został oszacowany na prawie 2 razy większej liczbie obserwacji niż model FE, gdyż model FE nie mógł zawierać żadnych obserwacji, dla których poziom handlu wynosił zero. Drugi powód podnoszą Shepherd i in. (2019), stwierdzając, że w modelach grawitacyjnych szacowanych MNK reszty w modelu ulegają specjalnej heteroskedastyczności, związanej z przekształceniem logarytmicznym zmiennych. Niestety zastosowanie macierzy odpornych nie niweluje tych problemów. Oceniając wpływ odległości na wzajemny handel między państwami należy raczej skupić się na oszacowaniach modelu PFE.
| brak danych | FE (2) | CRE (3) | PFE (5) |
|---|---|---|---|
| Stała | brak danych | –16,99*** (0,24) |
brak danych |
| Log. PKB eksportera | 0,39*** (0,02) |
0,39*** (0,02) |
0,19*** (0,00) |
| Log. PKB importera | 0,68*** (0,02) |
0,68*** (0,02) |
0,36*** (0,00) |
| Log. PKB per capita eksportera | 0,16*** (0,02) |
0,16*** (0,02) |
0,34*** (0,00) |
| Log. PKB per capita importera | 0,09*** (0,02) |
0,09*** (0,02) |
0,22*** (0,00) |
| Log. odległości | –0,18 (0,17) |
–0,18 (0,17) |
–0,28*** (0,00) |
| Eksporter członkiem UE | 0,33*** (0,02) |
0,33*** (0,02) |
0,32*** (0,00) |
| Importer członkiem UE | –0,04* (0,02) |
–0,04* (0,02) |
0,12*** (0,00) |
| Wspólna granica | brak danych | 0,99*** (0,09) |
brak danych |
| Wspólny język | brak danych | 0,48*** (0,04) |
brak danych |
| Wspólny kolonizator | brak danych | 0,99*** (0,05) |
brak danych |
| Powiązania kolonialne po 1945 | brak danych | 0,98*** (0,11) |
brak danych |
| Wspólne źródła systemu prawnego | brak danych | 0,12*** (0,03) |
brak danych |
| Between(lnGDP_o) | brak danych | 0,72*** (0,02) |
brak danych |
| Between(lnGDP_d) | brak danych | 0,20*** (0,02) |
brak danych |
| Between(lnGDP_cap_o) | brak danych | –0,09*** (0,03) |
brak danych |
| Between(lnGDP_cap_d) | brak danych | –0,06* (0,03) |
brak danych |
| Between(lnDIST) | brak danych | –0,99*** (0,17) |
brak danych |
| Between(eu_o) | brak danych | –0,37*** (0,04) |
brak danych |
| Between(eu_d) | brak danych | –0,15*** (0,04) |
brak danych |
| Liczba obserwacji | 291543 | 291543 | 589176 |
| R2 | 0,25 | 0,32 | brak danych |
| Adj. R2 | 0,21 | 0,32 | brak danych |
| Log Likelihood | brak danych | brak danych | –9394974978,94 |
| AIC | brak danych | brak danych | 18789949971,88 |
Objaśnienia: ***p < 0,001; **p < 0,01; *p < 0,05.
Źródło: opracowanie własne.
Oszacowanie najpełniejszego modelu CRE, w którym ujęto zmienne stałe w czasie, przedstawia tabela 2. Zawarto w niej również odpowiadające modelowi CRE modele FE i PFE rozszerzone o pozostałe zmienne, które nie są stałe w czasie. Co pierwsze rzuca się w oczy, to oszacowania Modelu 2 i Modelu 3 odnośnie do zmiennych, które nie są stałe w czasie, są identyczne zarówno co do ich wartości, jak i co do ich błędów standardowych. Model 3 zawiera ponadto efekty between dla zmiennych, które nie są stałe w czasie.
Analizując wpływ logarytmu PKB na eksport, to w Modelach 2, 3 i 5 rozmiar gospodarek zarówno eksportera, jak i importera mają pozytywny znak i są istotne statystycznie. Wpływ ten jest jednak wyraźnie mniejszy w oszacowaniach Modelu 5. Jednakże to w Modelu 5 (PFE) wpływ średniej zamożności społeczeństwa, czyli PKB per capita, jest silniejszy niż w Modelach 2 i 3. W wszystkich modelach z tabeli 2 wpływ tych zmiennych jest jednak istotny statystycznie na poziomie 0,1%.
Zmienna logarytm odległości okazała się istotna statystycznie tylko w Modelu 5, a przyczyny tego muszą być podobne do tych opisanych powyżej, przy analizie oszacowań modeli „oszczędnych” tylko z 3 zmiennymi objaśniającymi (Modele 1 i 4).
Zastanawiające są też oszacowania wpływu członkostwa w Unii Europejskiej na poziom handlu pomiędzy państwami. Modele 2, 3 i 5 zgodnie wskazują, że jeśli państwo-eksporter jest członkiem UE, to eksportuje więcej niż gdyby nie było członkiem wspólnoty. Siła tego wpływu jest praktycznie identyczna w szacowanych modelach. Zostanie członkiem UE podnosi eksport o około (e0,32 – 1) * 100% ≈ 37,72% przy innych czynnikach niezmienionych. Wpływ członkostwa państwa importera w Unii Europejskiej nie jest jasny. Modele 2 i 3 sugerują, że nieznacznie zmniejsza to import (o około 4%). Jednakże Model 5 wskazuje, że ten wpływ jest pozytywny i wynosi około (e0,12 – 1) * 100% ≈ 12,75% przy innych czynnikach niezmienionych.
Teoretycznie można uzasadnić oba wyniki. Unia Europejska posiada wspólny system ceł oraz regulacji dotyczących importu. Standardy unijne dotyczące jakości produktów, zwłaszcza żywieniowych, są jednymi z najostrzejszych na świecie. Jednocześnie, dołączając do UE, inne państwa członkowskie nie są już objęte taryfami celnymi, więc mogą „wypychać” import z państw spoza wspólnoty.
Z drugiej strony dołączenie do UE wiąże się zazwyczaj ze wzrostem PKB i otrzymywaniem środków z Funduszu Spójności, co kolektywnie zwiększa poziom wydatków i powinno stymulować import w ogólności, nie tylko z państw wewnątrz UE. Z punktu widzenia ekonometrycznego problematycznym jest zidentyfikowanie przyczyn różnic oszacowań między Modelami 2 i 3 a 5. Może być to kwestia zdecydowanie szerszej próby przy estymacji Modelu 5. Wydaje się jednak, że dalsze badania są potrzebne w tym obszarze.
Zmienne stałe w czasie oszacowane Modelem 3 są istotne statystycznie i mają wartość dodatnią. Posiadanie wspólnej granicy zwiększa wzajemny handel średnio o około (e0,98 – 1) * 100% ≈ 166,45% przy innych czynnikach niezmienionych. Silny pozytywny wpływ mają też wspólny język używany przynajmniej przez część populacji obu państw. Ciekawym z punktu widzenia badań nad kolonializmem jest istotny statystycznie i bardzo silny wpływ zmiennych kolonialnych na handel wzajemny między państwami. Posiadanie wspólnego kolonizatora w przeszłości zwiększa wzajemny handel aż o około (e0,99 – 1) * 100% ≈ 169,12%. Podobny wpływ ma zachowywanie powiązań kolonialnych pomiędzy dwoma państwami po 1945 r.
Zbliżone systemy prawne, rozumiane jako wspólne źródła obecnych porządków prawnych, również mają istotny statystycznie pozytywny wpływ na handel między dwoma państwami. Podobieństwo systemów prawnych zwiększa wymianę handlową między partnerami o około (e0,12 – 1) * 100% ≈ 12,75% przy innych czynnikach niezmienionych.
6. Wnioski i podsumowanie
W artykule zweryfikowano sześć postawionych we wstępie hipotez. Wykazano, że rzeczywiście PKB eksportera i importera są istotnymi predykatorami poziomu handlu (H1). Co ciekawe, oszacowane wartości współczynników przy tych zmiennych sugerują, że większy wpływ na wymianę handlową ma PKB importera. Model 5 sugeruje, że wzrost PKB eksportera o 1% zwiększy wymianę handlową średnio o (e0,19 – 1) * 1% ≈ 0,21%, a PKB importera prawie 2 razy więcej – o (e0,36 – 1) * 100% ≈ 0,43%. Podobne jakościowo wnioski wynikają z innych modeli. Kolejna tradycyjna zmienna – odległość między państwami – okazała się wpływać na poziom handlu w sposób nieoczywisty. Znaczenie odległości różniło się pomiędzy modelami, ale można z ostrożnością przyjąć (na podstawie Modeli 4 i 5 oszacowanych na większej próbie), że odległość wpływa negatywnie na handel w sposób istotny.
Pozytywnie zweryfikowano hipotezę H2, że zamożność społeczeństwa (mierzona poprzez PKB per capita) pozytywnie wpływa na wymianę handlową. W tym przypadku zamożność mieszkańców państwa eksportera ma większy wpływ niż importera, co wydaje się zaskakujące. Wzrost PKB per capita eksportera o 1% zwiększa wymianę handlową średnio o (e0,34 – 1) * 1% ≈ 0,40%, podczas gdy importera o (e0,22 – 1) * 1% ≈ 0,25% (opierając się na Modelu 5).
Zgodnie z intuicją i literaturą wykazano również, że wspólna granica zwiększa poziom handlu między dwoma państwami, pozytywnie weryfikując hipotezę H3. Wpływ ten jest bardzo silny – posiadanie wspólnej granicy podwyższa handel średnio aż o (e0,99 – 1) * 100% ≈ 169,12%.
Na podstawie Modelu 3 należy przyjąć także hipotezę H5. Posługiwanie się tym samym językiem przez obywateli obu państw zwiększa wzajemny handel średnio o (e0,48 – 1) * 100% ≈ 61,61%. Niniejsze badanie potwierdza też znany trend ponadprzeciętnego poziomu handlu pomiędzy państwami europejskimi a ich koloniami (por. Kleiman 1976). Co ciekawe, wykazano, że handel pomiędzy koloniami, które w przeszłości były zależne od jednego mocarstwa, jest wyższy niż w przeciwnym przypadku. Kilkadziesiąt lat po uzyskaniu niepodległości zaszłości historyczne nadal mają znaczenie dla poziomu handlu.
Ponadto badanie stanowi argument, że zbliżone systemy prawne skutkują większą wymianą handlową pomiędzy dwoma państwami, co potwierdza prawdziwość hipotezy H6. Zależność ta jest jednak zdecydowanie słabsza od wpływu zmiennych politycznych (wspólny kolonizator), społecznych (wspólny język) i naturalnych (wspólna granica).
Nieoczywiste wnioski dotyczą zwłaszcza członkostwa w Unii Europejskiej (hipoteza H4). Potwierdzono w tym artykule, że obecność w UE państwa eksportera zwiększa jego eksport. Wpływ członkostwa na import jest jednak niejednoznaczny i wymaga dalszych badań.
Z punktu widzenia metodologii wartością dodaną pracy jest zwłaszcza to, że pokazano, iż warto stosować różne metody ekonometryczne do badania determinantów handlu. Modele CRE i PFE okazały się użytecznymi narzędziami do estymacji modeli grawitacyjnych handlu, rozwiązując problem zmiennych stałych w czasie oraz problem zerowych wartości zmiennej objaśnianej. Pozwoliło to na włączenie do analizy większej liczby zmiennych (modele CRE), a także więcej obserwacji (modele PFE). Wszystkie obliczenia zawarte w artykule są w pełni replikowalne i mogą stanowić inspirację dla kolejnych badaczy w innych projektach naukowych.
Autorzy
* Tymoteusz Mętrak
Bibliografia
Ambroziak Ł. (2018), Determinanty handlu zagranicznego Polski mierzonego wartością dodaną, „Przedsiębiorczość Międzynarodowa”, 4(1): 9–22. https://doi.org/10.15678/PM.2018.0401.01
Anderson J.E. (2011), The Gravity Model, „Annual Review of Economics”, 3(1): 133–160. https://doi.org/10.1146/annurev-economics-111809-125114
Baltagi B.H. (2021), Econometric Analysis of Panel Data, Springer. https://doi.org/10.1007/978-3-030-53953-5
Bergstrand J.H., Egger P. (2013), Gravity Equations and Economic Frictions in the World Economy, [w:] D. Bernhofen, R. Falvey, D. Greenaway, U. Kreickemeier (red.), Palgrave Handbook of International Trade, Palgrave Macmillan UK, s. 532–570. https://doi.org/10.1007/978-0-230-30531-1_17
Bułkowska M. (2018), Model grawitacyjny w handlu zagranicznym: Wybrane aspekty teoretyczne i metodyczne, „Prace Naukowe Uniwersytetu Ekonomicznego we Wrocławiu”, 529: 39–47. https://doi.org/10.15611/pn.2018.529.03
Chamberlain G. (1984), Panel data, [w:] Z. Griliches, M. Intriligator (red.), Handbook of Econometrics, s. 1247–1318.
Cieślik A. (2007), Wpływ porozumień o wolnym handlu na wielkość wymiany handlowej Polski w latach 1992–2004, „Bank i Kredyt”, 6: 3–23.
Cieślik A. (2018), Determinanty bilateralnych obrotów handlu zagranicznego Polski: Czy integracja europejska ma znaczenie?, „Przedsiębiorczość i Zarządzanie”, 19(2.2): 23–34.
Cieślik A., Hagemejer J. (2011), The Effectiveness of Preferential Trade Liberalization in Central and Eastern Europe, „The International Trade Journal”, 25(5): 516–538. https://doi.org/10.1080/08853908.2011.604298
Cieślik A., Michałek J., Mycielski J. (2009), Prognoza skutków handlowych przystąpienia do Europejskiej Unii Monetarnej dla Polski przy użyciu uogólnionego modelu grawitacyjnego, „Bank i Kredyt”, 40(1): 69–88.
Conte M., Cotterlaz P., Mayer T. (2022), The CEPII Gravity database (Working Paper No. 2022-05), Centre d’Etudes Prospectives et d’Informations Internationales.
Drzewoszewska N., Pietrzak M.B., Wilk J. (2013), Grawitacyjny model przepływów handlowych między krajami Unii Europejskiej w dobie globalizacji, „Roczniki Kolegium Analiz Ekonomicznych”, 30: 187–202.
Golovko A., Sahin H. (2021), Analysis of International Trade Integration of Eurasian Countries: Gravity Model Approach, „Eurasian Economic Review”, 11(3): 519–548. https://doi.org/10.1007/s40822-021-00168-3
Hausman J.A., Taylor W.E. (1981), Panel Data and Unobservable Individual Effects, „Econometrica”, 49(6): 1377–1398. https://doi.org/10.2307/1911406
Head K., Mayer T. (2014), Gravity Equations: Workhorse, Toolkit, and Cookbook, [w:] G. Gopinath, E. Helpman. K. Rogoff (red.), Handbook of International Economics, Oxford: Elsevier, s. 131–195. https://doi.org/10.1016/b978-0-444-54314-1.00003-3
Kepaptsoglou K., Karlaftis M.G., Tsamboulas, D. (2010), The Gravity Model Specification for Modeling International Trade Flows and Free Trade Agreement Effects: A 10-Year Review of Empirical Studies, „The Open Economics Journal”, 3(1): 1–13. https://doi.org/10.2174/1874919401003010001
Kleiman E. (1976), Trade and the Decline of Colonialism, „The Economic Journal”, 86(343): 459–480. https://doi.org/10.2307/2230793
Klimczak Ł. (2015), Model grawitacyjny jako narzędzie analizy handlu zagranicznego, „Zeszyty Naukowe Uniwersytetu Ekonomicznego w Krakowie”, 5(941): 107–130. https://doi.org/10.15678/ZNUEK.2015.0941.0508
Kułyk P., Augustowski Ł. (2018), Zastosowanie modeli grawitacyjnych dla wybranych zbóż w handlu między UE a USA, „Zeszyty Naukowe SGGW w Warszawie – Problemy Rolnictwa Światowego”, 18(4): 295–303. https://doi.org/10.22630/PRS.2018.18.4.119
Linders G.-J.M. (2005), Distance Decay in International Trade Patterns – a Meta-analysis, 45th Congress of the European Regional Science Association: „Land Use and Water Management in a Sustainable Network Society”, 23–27 August 2005, Amsterdam, The Netherlands, European Regional Science Association (ERSA), Louvain-la-Neuve.
Maciejewski M. (2017), Determinanty wykorzystania czynników wytwórczych w strukturze eksportu państw Unii Europejskiej, „Horyzonty Polityki”, 8(22): 131–149.
Maciejewski M., Wach K. (2019). What Determines Export Structure in the EU Countries? The Use of Gravity Model in International Trade Based on the Panel Data for the Years 1995–2015, „Journal of International Studies”, 12(1): 151–167. https://doi.org/10.14254/2071-8330.2019/12-1/10
Mroczek K., Tokarski T., Trojak M. (2014), Grawitacyjny model zróżnicowania rozwoju ekonomicznego województw, „Gospodarka Narodowa”, 271(3): 5–34. https://doi.org/10.33119/GN/100867
Mundlak Y. (1978), On the Pooling of Time Series and Cross Section Data, „Econometrica”, 46(1): 69–85. https://doi.org/10.2307/1913646
Pietrzak M.B., Łapińska J. (2014), Zastosowanie modelu grawitacji do identyfikacji czynników determinujących przepływy handlowe w Unii Europejskiej, „Przegląd Statystyczny”, 61(1): 65–77.
Popovych A. (2018), Zastosowanie modelu grawitacyjnego do analizy międzynarodowego handlu miodem pszczelim, „Zeszyty Naukowe SGGW w Warszawie – Problemy Rolnictwa Światowego”, 18(4): 395–406. https://doi.org/10.22630/PRS.2018.18.4.128
Sapa A., Droždz J. (2019), Polish Agri-Food Trade with Non-EU Countries – A Gravity Model Analysis, „Annals of the Polish Association of Agricultural and Agribusiness Economists”, XXI(4): 403–412. https://doi.org/10.5604/01.3001.0013.6006
Sapa A., Kryszak Ł. (2021), Processed Food Trade of European Union Countries – The Gravity Approach, „Annals of the Polish Association of Agricultural and Agribusiness Economists”, XXIII(2): 96–108. https://doi.org/10.5604/01.3001.0014.8975
Shepherd B., Doytchinova H.S., Kravchenko A. (2019), The Gravity Model of International Trade: A User Guide [R version], Bangkok: United Nations ESCAP, https://www.unescap.org/resources/gravity-model-international-trade-user-guide-r-version (dostęp: 30.09.2024).
StataCorp (2023), Stata 18 Longitudinal-Data/Panel-Data Reference Manual, College Station, xthtaylor, TX: Stata Press.
Tinbergen J. (1962), Shaping the World Economy: Suggestions for an International Economic Policy, New York: The Twentieth Century Fund.
United Nations Department of Economic and Social Affairs (2019), World Urbanization Prospects: The 2018 Revision, United Nations.
Wooldridge J.M. (2021), Two-Way Fixed Effects, the Two-Way Mundlak Regression, and Difference-in-Differences Estimators, Rochester, NY. https://doi.org/10.2139/ssrn.3906345
Przypisy
- 1 Wartość 300 000 mieszkańców nie jest ustalona arbitralnie, a pochodzi z opracowania Organizacji Narodów Zjednoczonych, która tak właśnie definiuje duże miasto (World Urbanization Prospects 2018).
